Models and Methods with Applications in Neuroscience
Publications
- In progress: Chen, Y. and S. T. Tokdar. Bayesian estimation of block correlation matrices with an unknown block assignment
- In progress: Chen, Y. and S. T. Tokdar. Modeling neural population coordination via a block correlation matrix of fluctuating weights (poster)
- In progress: Chen, Y. and S. T. Tokdar. Testing among different types of second of stochasticities
Phase 1: Single neuron present Mixture pattern
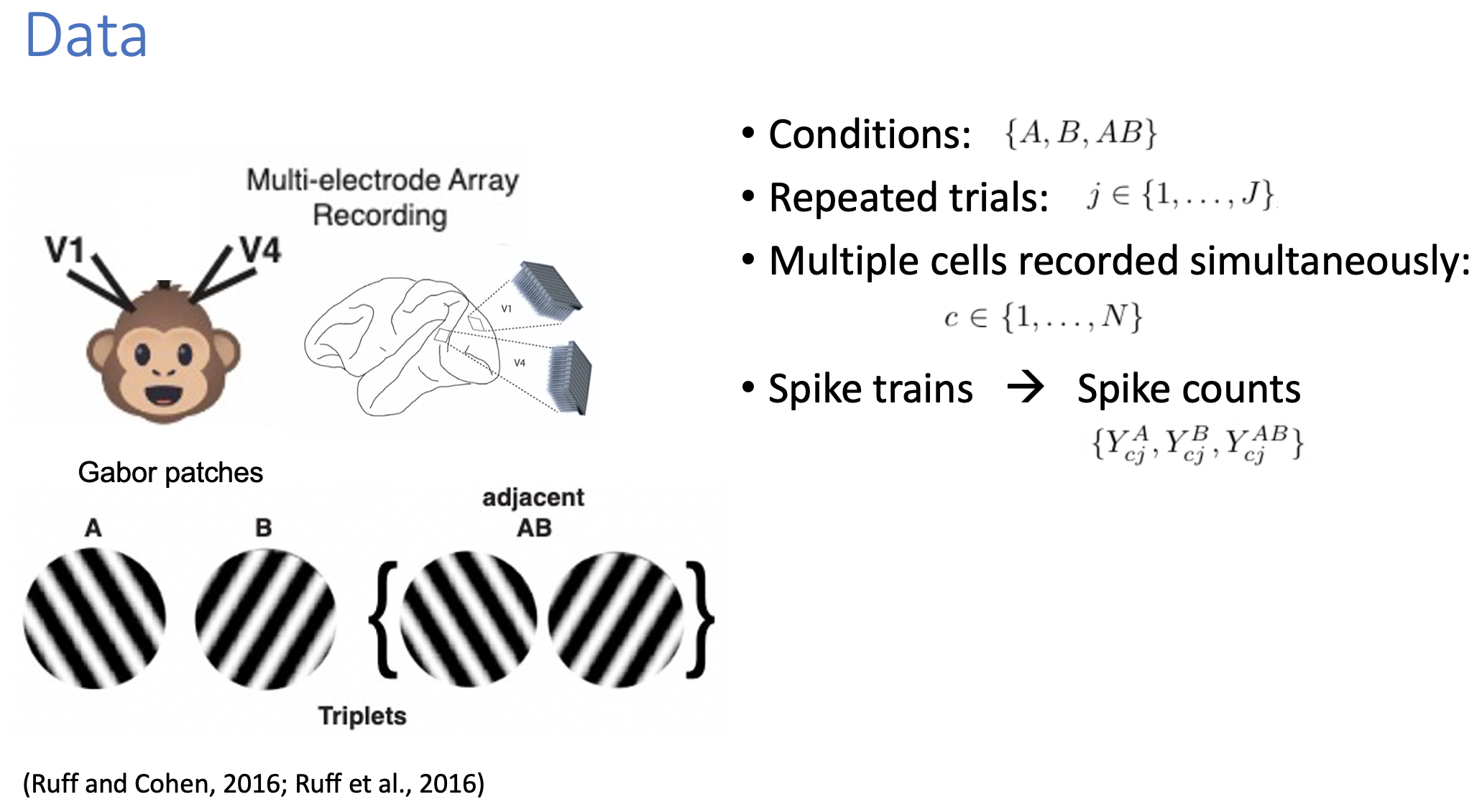
Experiment Design
How neural population preserves multiple simultaneously presented stimuli is a fundamental question, but has not yet been fully understood by neuroscientists. A popular hypothesis is that individual neuron is designated for each signal. However, receptive fields of visual and auditory neurons are shown to be large, suggesting a single neuron may be exposed to multiple stimuli simultaneously (Groh et al., 2003; Werner-Reiss and Groh, 2008; Bulkin and Groh, 2011). In this case, a single neuron cannot respond to only a single stimulus based on perceptual sensitivity, but presents a dynamic between multiple stimuli. Caruso et al. (2018) suggest a ‘Mixture’ dynamic under dual stimuli, where a single neuron may encode information by fluctuating between two stimuli from trials to trials. And they further show a neuron may present a ’time division multiplexing’ within a trial (Caruso et al.,2018; Glynn et al.,2021; Mohl et al., 2020).
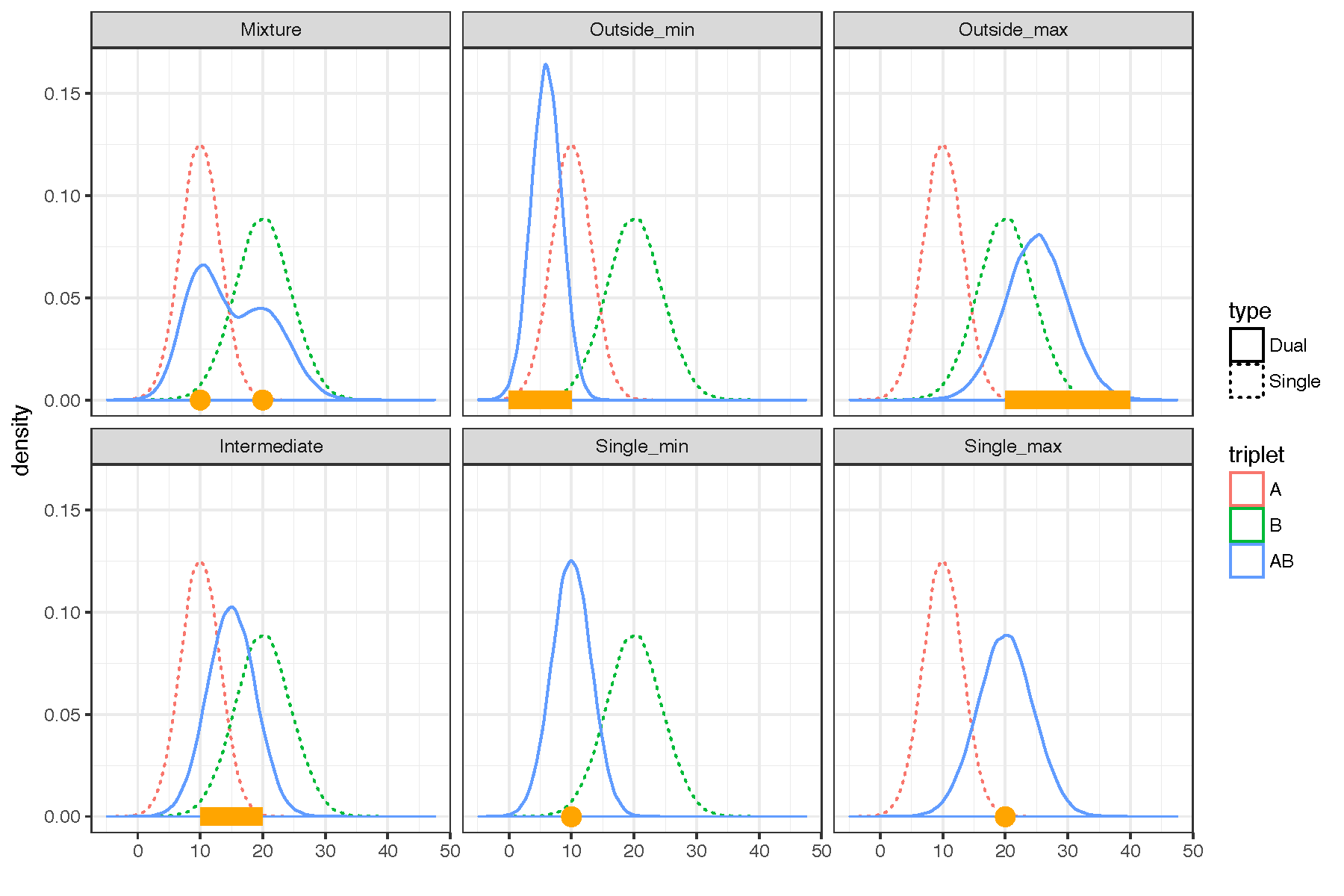
Four biological-meaningful modes of second order variations.
We define four types of Poisson mixtures to represent potential second order stochasticity manifested in a single neuron’s activation patterns. We aim to develop a hypothesis testing to test among distinct compting modes of second order stochastic variations. Under a Bayesian paradigm, the testing requires an integration of an infinite-dimensional nonparametric mixing distribution for the marginal likelihood estimation, bringing a practicability challenge. We circumvent this computing problem by adopting a pseudo-Bayesian framework of Predictive Recursion Marginal Likelihood (PRML) proposed by Martin and Tokdar (2011) and design a PRML-based test. We analyze spike trains of a single neuron in the inferior colliculus region, suggesting a single neuron in dual-stimuli trials does exhibit a second order stochasticity by randomly interweaving between constituent signals.
Phase 2: Neural coordinaton on turn-taking selection
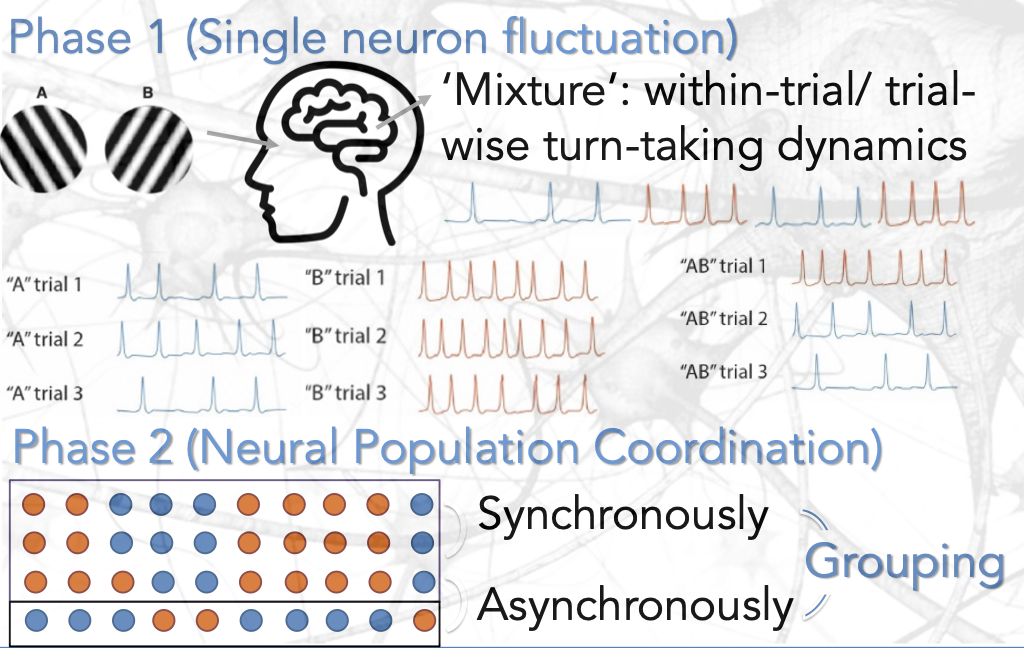
Neural Coordination of turn-taking signal-selection activities
Turn-taking activities presented by individuals are shown to present a coordination pattern in neural population (Jun et al., 2019). Intuitively, neural population may present clustering behaviors in their coordination activities. Firstly, there must exist asynchronous selection processes of stimuli among neurons to ensure that every stimulus in each trial is encoded by at least one neuron. Secondly, there may also exist synchronous selection processes of stimuli between two neurons which both act opposite to the same neuron, or as a result of other possible hypothesis such as sub-optimal computation and so on. Such asynchronization and synchronization may shape neural population into different clusters in neural population. Apart from groups of neurons selecting signals (a)synchronously, we may also expect a group of neurons act insensitively to signals, presenting a small correlation to selection activities with other neurons. These possibilities require an estimation of a block correlation matrix.
A block correlation matrix not only contributes to depict possible scenarios in neural population coordination, but also helps to improve statistical efficiency in a large p small n settings. In our motivated example (Ruff and Cohen, 2016; Ruff et al., 2016), a Utah array is used to deliver 100 neural signals simultaneously. On the contrary, the number of repeated trials is relative smaller compared to the number of recorded neurons, ranging from 20 to 70.
We consider a block structure on a correlation matrix to enjoy both interpretability and statistical efficiency. To circumvent intractable normalising constraints calculation resulting from block structure and valid correlation matrix constraints, we propose a novel model based on the canonical representation (Archakov and Hansen, 2020) in a Bayesian framework. I also incorporate a mixture of finite mixtures model (Miller and Harrison, 2018) to allow for estimating unknown block structure. We design a Gibbs sampling scheme where the parameters are updated by conjugacy.
- Posted on:
- July 29, 2022
- Length:
- 4 minute read, 655 words
- Categories:
- Neuroscience Nonparametric Bayesian Bayesian Factor model
- See Also: